Put Call Parity
I have begun reading the book ‘Paul Wilmott Introduces Quatitative Finance’ by none other than- you guessed it- Paul Wilmott. In the second chapter the first interesting concept that I am yet to familiarise myself with is ‘Put-Call Parity’. This post is an attempt to overcome that. I shall try to answer as many questions I can pose for myself. Let’s first get the basics out of the way.
First thing first. A Put-Call parity is talking about the expected parity between a Put Option and a Call Option that needs to be maintained. In fact, it automatically gets maintained in a free market because if it does not, people start to take advantage of it and dynamically enforce the parity eventually. How do all these happen? We shall see now. Before we go into the details, let me define the technical terms in English.
Definitions in English 101
Options
Options are a type of contract between two parties. What is in this contract? The contract is often to buy/sell a product at a pre-determined price at a future date. How is it different from a Forward contract? Well, the owner of the Option contract, or simply Option, has merely the right but not the obligation to fulfill it. Freedom from this constraint comes at a price which the owner must pay to the writer/seller of the Option in the beginning.
One of the parties- let it be BB8 1- sells a contract to, say, L0-LA59 2. BB8 writes the Option to probably get access to some immediate money. L0LA, as the holder/buyer/owner of the Option, pays a premium to BB8 and acquires it. The Option is about buying gold at ₹5500/g after a year’s time. L0LA must think the price of gold is going to go way above ₹5500/g, so she pays a little premium now to keep the value fixed for herself. She may need to buy the gold to make jewelleries out of it. Or she may simply buy it at ₹5500 and immediately sell it at market price- which she thinks would be higher- to gain some profit. On the other hand, BB8 hopes that the market price of gold will not cross ₹5500, in which case the option will not be exercised at all and he gets to keep the premium L0LA paid him anyway.
A Call Option is an Option which will give the buyer the right to purchase something (this can be stock, another contract, commodities like gold and oil etc or a foreign currency) but not the obligation at the Expiry Date, otherwise known as the maturity date.
A Put Option gives the buyer the right to sell an underlying asset at the Strike Price i.e., the pre-determined price at maturity.
Long-Short Positions
Whoever buys the Option, be it Call or Put, is in the long position. The seller is at the short position. In the example above, BB8 is shorting a call option. Convince yourself of the following statements before we can proceed.
- A long position holder of a call option would want the underlying asset price, \(S(T)\), to be higher than the strike price, \(E\), at time \(T\).
- A long position holder of a put option would want \(S(T) < E\).
- A short position holder of a call option would want \(S(T) < E\).
- A short position holder of a put option would want \(S(T) > E\).
- If you’re shorting a call option, your gain is fixed at the premium obtained and loss is unlimited.
- If you’re shorting a put option, your gain is fixed at the premium but loss can be as high as the strike price \(E\).
- If you’re buying a call option, your gain is unlimited and loss is minimized to the premium value.
- If you are buying a put option, your gain is as high as \(E\) and loss is the premium price paid.
Let’s Arbitrage Not
Hedging is this beautiful technique that has been created to rescue the lives of investors. It is the process of minimizing risk in any investment. Because hedging is wanted by everybody, by default it means, there is also no way of making money free money (apart from due to the randomness inherent to the assets) either. This is called no arbitrage. These ideas influence what the premium price of Options should be. Not only that but also if the price of a call option is determined then so is the price of a put option, as long as they are being done for the same strike price for the same maturity date of the same underlying asset.
This is usually done by combining multiple assets such that they negate each other’s risk. Since we are noobs and have only learnt about Options and stocks so far, those are the things with which we shall try to construct a risk-free portfolio. Let’s see what happens if we combine two different types of Options first.
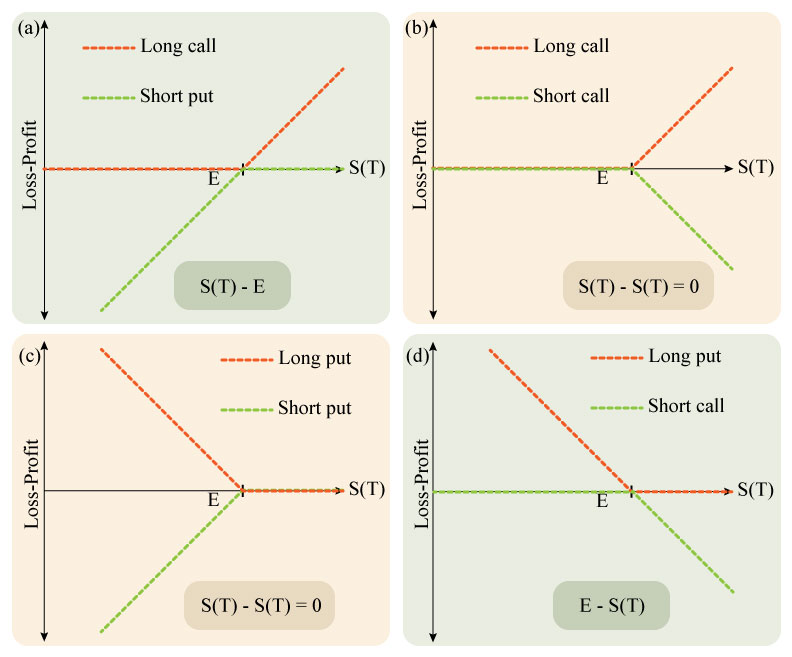
Time to dissect each diagram.
(a) L0LA has a long call and a short put. In descriptive words, she has bought a call options (from BB8) and sold a put option (to BB8). Both have the same underlying asset whose price varies as \(S(t)\). The strike price for both is \(E\). We are only seeing how much money she will have at maturity from each option. If \(S(T) > E\), she will choose to buy the underlying at \(E\) instead of \(S(T)\) because it is cheaper. She will exercise the call option at an immediate profit \(S(T)-E\). Otherwise, she will not exercise the call Option and instead have the loss amount equal to the premium she paid initially which is say, C.
If \(S(T) < E\), BB8 will want to exercise the put option because he wants to sell it at a higher price. Now L0LA will be in a loss equal to \(E-S(T)\) because she is obligated to fulfill BB8’s wish. So, no matter what the amount L0LA ends up with at \(T\) is equal to \(S(T)-E\).
Now let’s see what did she have to do initially to get there. What happens at \(t=0\) (current time) when the Option transactions takes place? L0LA buys call option at \(C\) and sells put option at \(P\). So, technically her money worth \(P-C\) became \(S(T)-E\) eventually. But there are other ways to get here. She can buys the asset at \(S(0)\) at \(t=0\) and borrow \(E e^{-r T}\) from the bank at risk-free rate of \(r\). So her current value at hand \(Ee^{-r T}-S(0)\) will become \(S(T)-E\) too at maturity. Then the two ways of gaining the same amount in future must also be same at current time.
The following equation defins the put-call parity.
\[\boxed{C - P = S(0) - E e^{-r T}}\]If this is not satisfied, arbitrage will become a possibility.
(b) If L0LA held both a long call and a short call option, her maturiy amount will simply cancel each other and the portfolio must also cost her nothing at present. It is simple to see as \(C-C=0\).
(c) BB8 has a long put and a short put. He is at the same situation as L0LA in (b).
(d) This is basically the opposite scenario of (a). BB8 has purchased a put option from L0LA and sold her a call option as well. The value he has spent is \(P-C\). By spending this money he will eventually get \(E-S(T)\). But this can also be gained by lending \(Ee^{-rT}\) and shorting the asset at \(S(0)\). The money he has currently spent by doing this is \(Ee^{-rT}-S(0)\). The two methods should be same and we gain back the put-call parity relationship.
Now I have a much better understanding compared to when I began writing the post. I hope the same happened to you too. Happy quantifying! (Dies cringing)